Elastic Networks

How elastic networks respond to deformation depends sensitively on both the properties of the constituent filaments and on the network topology. For the former, how individual filaments respond to being stretched or compressed affects the response at the network level. For the latter, important properties include how and where the filaments are connected.

My research focuses on using computer simulations of model networks to understand this behaviour and to find ways of controlling it, focusing in particular on so-called marginal networks.

Modelling elastics networks

Perhaps the simplest model elastic networks are lattice-based networks of Hookean springs. These are constructed by placing network nodes on lattice sites and then connecting all nearest neighbours with springs. The number of connections at each node is given by the connectivity z, and the initial value will depend on the lattice used. In 2d, for example, beginning from a triangular lattice will give z=6, while a square lattice has z=4. The network topology can then be controlled by randomly diluting the network. That is, by randomly removing springs one can control the value of z. Since we are using Hookean springs, the only response to deformation is when the springs are stretched or compressed.

This lattice based method can also be used in 3d, using, for example, simple cubic (z=6) or FCC (z=12) based lattices. Other, more complex network geometries include Mikado networks, where, as in the game, sticks of equal length are dropped randomly. Overlapping sticks are then cross-linked to form a network. The key parameter here is the density of sticks, which is controlled by randomly removing them. Even more removed from lattice based networks are so-called random-bond networks, where network nodes are placed randomly and randomly chosen pairs are then connected.

Model elastic network consisting of network nodes (red circles) connected by Hookean springs (blue lines)

Marginal networks: Highly responsive soft-matter materials

As filaments are removed from a network, it will become increasingly easier to deform it. Measures of a network's rigidity, such as the shear modulus G (defining how strongly the network resists shear deformation), will decrease as the connectivity z is decreased. If all excess filaments are removed the network will be at the point where it is just mechanically stable: remove one more filament and the network is under-constrained and can be deformed with no cost in energy; add one more filament, and the network is over-constrained and will be stable.

In 1864 Maxwell showed that this point is approximately reached when the number of degrees of freedom in the network (given by the number of network nodes) is just equal to the number of constraints (given by the springs connecting the nodes). In d dimensions this gives a critical connectivity between rigid and floppy networks of approximately z_c≈ 2d. When a network is at this so called Maxwell-point it is said to be a marginal network, since it is at the edge, or margins, of mechanical stability. Marginal networks have many interesting and potentially useful properties, as they are both unusually stiff and highly responsive to external forces or fields, properties which are desirable in smart materials (materials which are designed to have properties that can be significantly changed in a controlled manner). Much theoretical work has looked at how marginal networks respond to applied forces and fields.

Thermal fluctuations

Consider a network of springs at or below the marginal point. It costs no energy to apply a small deformation to such a network. However, by, for example, shearing the network, one reduces the number of states that the network can assume. This results in a decrease in the system entropy and hence an increase in the system free-energy. Therefore, while there is no energy cost associated with (small) network deformations, there is a free energy cost, meaning that the network will begin to resist deformation. Based on the idea of entropic elasticity, when one considers a mechanically floppy network the strength of the response to deformation is expected to scale linearly with the temperature, and to be independent of the mechanical energy of the spring, defined by its spring constant k.

Using Monte Carlo simulations, it is possible to take thermal fluctuations into account when modelling elastic networks. While it is indeed the case that sub-marginal networks exhibit a linear response, that is G ∝ T, with no dependence on k, marginal networks exhibit a response whose dependence on temperature is sub-linear. Triangular-lattice based networks diluted to the marginal point exhibit a shear modulus that scales as G ∝ T^1/2k^1/2. This not only gives two control parameters for the network response, namely the spring constant and the temperature, but also results in a network that has an anomalously high rigidity. That is, when dealing with small temperatures, sub-linear powers result in larger values of G. Such results are not limited to lattice based networks: random bond networks exhibit the same qualitative behaviour, albeit with a different scaling constant, with G ∝ T^2/3k^1/3.

Viscoelastic networks: dynamical behaviour

Another interesting aspect of marginal networks is their behaviour in the presence of a solvent. When a dynamical shear (e.g. a shear strain with a fixed amplitude which oscillates with frequency ω) is applied to a network in a fluid, a viscous drag will act on it. Furthermore, as the network collide with the fluid particles it generates a hydrodynamic flow field, allowing the network filaments to interact with each other via the fluid. For such a dynamically oscillating system one can measure the dynamical shear modulus G^* = G^' + G^'', with G^' the storage modulus (the stored energy, i.e. the elastic part from the springs) and G^'' the loss modulus (the energy dissipated as heat, i.e. the viscous part).

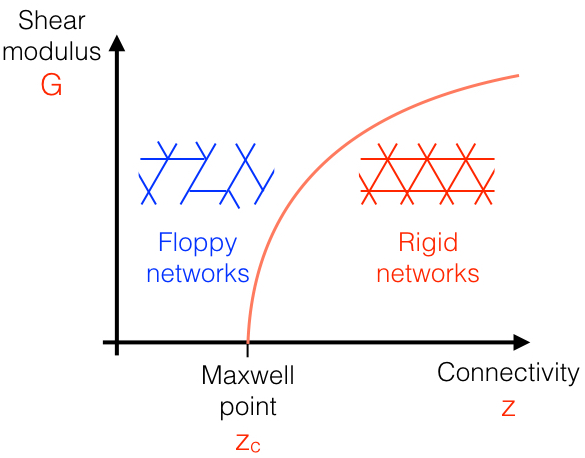
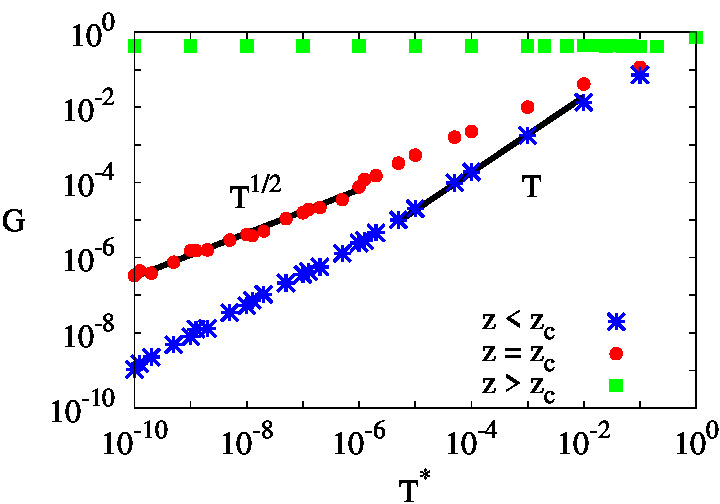
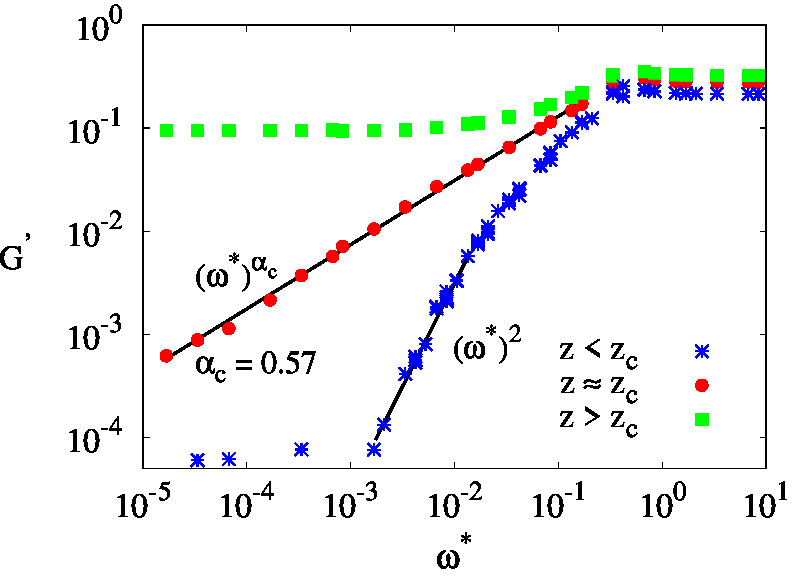
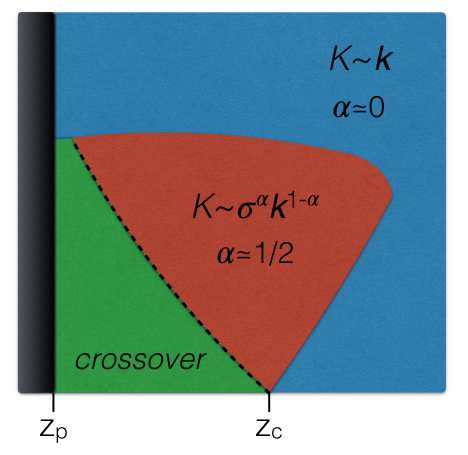
For networks which are mechanically floppy one would expect the modulus to behave as a Maxwell fluid, where the storage modulus, for example, scales with the shear frequency as G^' ∝ ω². Using computer simulations we show that this is indeed the case for sub-marginal networks. For marginal networks, however, one finds, as for temperature, a sub-linear scaling, with G^' ∝ ω^αk^1-α, with α<1, again resulting in a network which is anomalously rigid. Interestingly, the exponent α depends on the strength of the hydrodynamic interactions between the network nodes, and can in fact be controlled by varying parameters such as the density of the fluid, giving another potential control parameter for the system behaviour.

And in reality: Detecting marginal networks in experiments

While marginal networks could potentially be very useful materials, experimental evidence for the critical behaviour associated with them has thus-far been limited. It is firstly very difficult to create a network whose connectivity is at or close to the marginal point. Secondly, simulation and theoretical evidence indicates that the interesting behaviour occurs when the constituent filaments are relatively stiff. Synthetic polymer networks tend to allow for greater control over the network topology, but they tend to be relatively soft. Biopolymers are much stiffer, but one has less control over the network topology. Recent advances in the production of synthetic polymers have produced networks that are of comparable stiffness to biopolymer networks, while allowing for control over the network topology, potentially paving the way for producing marginal networks.

This still leaves the question of how to detect marginal networks. One solution would be to look for signs of marginal behaviour in the network's response to deformation. Unsurprisingly, it is not really feasible in experiments to vary parameters such as the temperature by the many orders of magnitude that is possible in computer simulations. However, one parameter which can be varied over a sufficiently large range is the shear stress σ. Using both experimental studies and computer simulations we have found that the response of networks of synthetic semi-flexible polymer to shear stress exhibits marginal-like behaviour, scaling as G^' ∝ σ^αk^1-α, even in networks well below the marginal point, giving the first experimental evidence for such behaviour in filamentous polymer networks.

Matthew Dennison

Elastic Networks